
Une famille doit traverser une rivière, mais il n’y a qu’une petite barque !
Le père pèse 80 kg, la mère 75, le fils 40 kg, la fille 38, le petit chien 5 kg environ;
mais surtout le chargement de la barque est limité à 80 kg strictement !
Comment faire traverser toute la famille ?
( on ne peut pas nager …)
Les problèmes de passage de rivière sont des exercices relevant de jeux mathématiques ou de réflexions. Certains sont très anciens, tels ceux posés au VIIIe siècle par l’abbé de Cantorbéry, Alcuin, dont le plus connu est le problème du loup, de la chèvre et des choux. Plus récemment, au XVIIIe siècle, les habitants de Koenigsberg, en Prusse-Orientale, se demandèrent s’il était possible de passer tous les ponts de leur ville sans jamais emprunter deux fois le même chemin. Le mathématicien Leonhard Euler examina le problème, en démontra l’impossibilité, et fonda la topologie, nouvelle discipline de mathématiques. Ce problème est dénommé problème des sept ponts de Königsberg. Ce type de problème présente encore aujourd’hui un intérêt mathématique en lien avec la théorie des graphes.
Solution de la récré précédente: Fabrication d’une boîte à tapioca
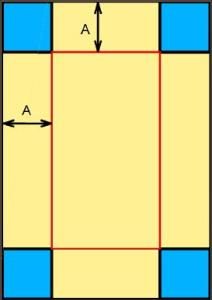
Plusieurs raisonnements sont possibles, suivant son envie et son niveau en maths.
Comme Pierre, on peut faire des essais avec du papier, des ciseaux et du scotch, et trouver petit à petit la meilleure solution. Les 3 essais de Pierre nous montrent que le volume maximum est supérieur ou égal à 1,06 litre.
Comme Jean, on peut trouver la formule donnant le volume de la boîte en fonction de A.
En effet, ce volume est égal à la hauteur de la boîte que multiplie la surface de sa base, c’est à dire sa largeur multipliée par sa longueur. La feuille de papier étant de dimension 21 x 29.7cm, le schéma nous permet de vérifier que la hauteur vaut A, la largeur vaut 21 – (2xA), et la longueur 29.7 – (2xA).
Donc le volume de la boite (en cm3) vaut : A x (21 – 2xA) x (29.7 – 2xA)
Ensuite, deux façons de faire : essayer plusieurs valeurs de A pour trouver petit à petit la meilleure solution. Ou bien se souvenir des maths du lycée pour trouver la formule exacte donnant la meilleure valeur de A. Allons-y…
Le volume est une fonction de A : V(A) = Ax(21 – 2xA)x(29.7 – 2xA) , avec A compris entre 0 et 10.5 cm. (2xA ne pouvant dépasser la largeur 21). On peut encore la réécrire sous la forme :
V(A) = 4 A3 – 101.4 A2 + 623.7 A
Si on trace la courbe de ce volume en fonction de la longueur A, on voit intuitivement la solution :
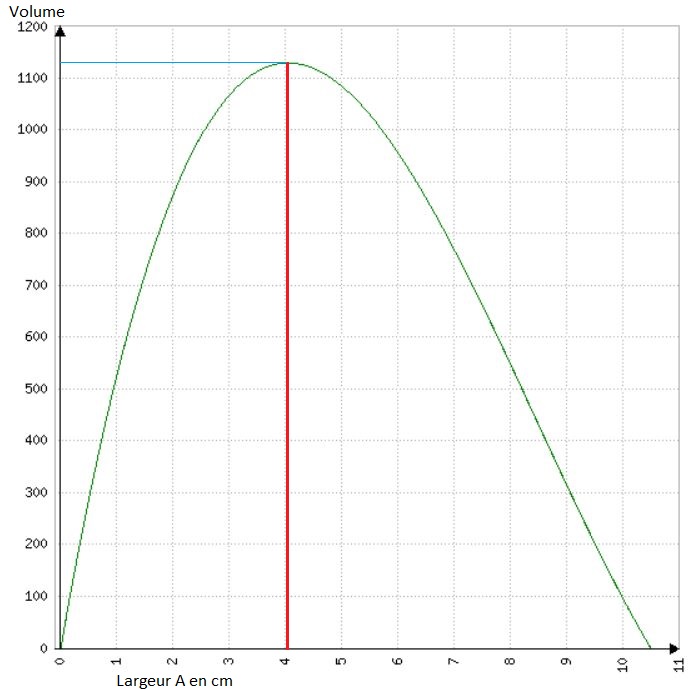
Le volume maximum est atteint lorsque A vaut environ 4 cm
Encore un peu plus de mathématiques (courage !) :
C’est un polynôme de degré 3. Sa valeur maximale sur [0 ; 10.5] sera atteinte soit aux bornes de l’intervalle (c’est à dire en A=0 ou en A= 10.5), soit en un point où la dérivée est nulle (au sommet de la bosse).
La dérivée vaut : V’(A) = 12 A2 – 202,8 A + 623,7. (jusqu’ici tout va bien)
C’est un polynôme de degré 2, c’est-à-dire une parabole. Son discriminant vaut D = 202,82 – 4 x 12 x 623,7 = 11190,24.
Puisqu’il est positif, le polynôme a 2 racines (c’est-à-dire 2 valeurs qui l’annulent), qui valent respectivement (202,8 – racine(D))(2 x 12) et (202,8 + racine(D))(2 x 12) , c’est-à-dire 4,0423… et 12,8576…
La dérivée V’(A) est positive pour A inférieur à 4,0423 et A supérieur à 12,8576 , et négative pour A compris entre 4,0423 et 12,8576. Donc le volume V(A) est une fonction croissante pour A inférieur à 4,0423 , décroissante pour A compris entre 4,0423 et 12,8576, puis à nouveau croissante pour A supérieur à 12,8576. Elle admet donc un maximum en A= 4,0423 , qui est bien une valeur autorisée pour A (car entre 0 et 10,5).
Le volume maximum est donc V(4,0423…) = 1 128,495 cm3 = 1,128 litre

