15 boules identiques ont toutes la même masse, sauf une.
On a effectué 3 pesées avec une balance à plateaux:
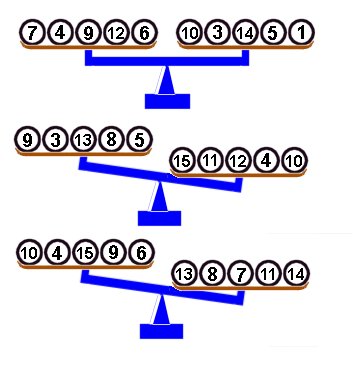
Quelle est la boule qui n’a pas la même masse que les autres ?
Attention, on ne sait pas si elle est plus lourde ou plus légère
Et la solution de l’énigme précédente: (aimablement fournie par notre Président, merci Christine!)
Décomposer l’âge de Loulou en facteur premier.
1°) on suppose que la décomposition commence par 2, l’age est pair. Donc les 3 nombres a,b,c sont pairs car chacun se retrouve en unité sur 2 permutations. On a donc pour abc le choix entre 2,4,6, et 8.
Si 2 est facteur double (age de Loulou multiple de 4) : le nombre à 2 chiffres des deux derniers nombres (dizaine et unité) doit être multiple de 4. Pour abc, on doit avoir bc multiple de 4. C’est impossible car bc=42 ne va pas, bc=26 non plus ni bc=46. Donc aucun triplet de 2,4,6,8 ne convient.
Si 3 est le deuxième facteur premier, alors la somme a+b+c doit être multiple de 3. On a donc soit a+b+c=12, soit a+b+c=18. ce qui donne (a,b,c)=(2,4,6) ou (a,b,c)=(4,6,8).
Avec (2,4,6) : 246=6×41 ce qui conduit à un âge de 6 pour Loulou (41 est un nombre premier). Impossible.
Avec (4,6,8) : tout marche et on obtient Loulou a 18 ans et les potes 26, 27, 36, 38, 47, 48.
Reste à montrer qu’il n’y en a pas d’autres….
Avec l’âge pair pour Loulou : 2×5 ne va pas, les autres âges seraient tous multiples de 10. On peut d’ailleurs éliminer 5 comme facteur car tous les autres âges se termineraient par 0 ou 5.
On essaie 2×7 : trop petit comme cela pour Loulou et trop grand si on multiplie par un autre facteur (plus grand que 7).
Donc on a fini avec le cas pair.
2) Cas impair : on a comme possibilités pour a,b,c 1,3,5,7,9. Les 3 nombres a,b e c doivent être impairs.
facteur 3×5 : non à cause du 5
facteur 3×7 (Loulou aurait 21 ans) : abc divisible par 3 : ‘ cas possibles : (1,3,5), (1,5,9), (3,5,7) et (5,7,9). il faut que abc et toutes les permutations soient divisibles par 7. Critère de divisibilité : le nombre des dizaines moins 2 fois le « chiffres » des unités divisibles par 7.
(1,3,5) prenons 135 : 13-2×5=3 pas divisible par 7.
(1,5,9) prenons 591 : 59-18=41 pas divisible par 7.
(3,5,7) prenons 375 : 37-10=27 pas divisible par 7
(5,7,9) prenons 579 : 57-18=39 pas divisible par 7.
donc pas de solution.
facteur 3×11 : trop grand pour l’âge de Loulou (qui est le plus jeune).

