 Saurez-vous retrouver tous les noms de mathématiciens cachés dans le texte ?
Saurez-vous retrouver tous les noms de mathématiciens cachés dans le texte ?
Quittant son lit de l’hôpital pour ce weekend Pascal, Sophie Kovalewski avait les idées claires au point de ne plus se poser de questions, elle allait déclarer la guerre à ce gros poisson, ce Lobatchevski pour qui son antipathie du premier moment tournait en haine farouche. C’était le gendre d’un gros bras de la mafia russe, un ermite qui avait un fort accent gallois et une voix d’enrhumée : « C’est le monde à l’enbers, cette bauviète de fille bonne à chi, m’accuser de meurtre » menaçait-il brandissant sa canne, frêle sur ces jambes de héron…
La belle Sophie monta dans sa Ferrari, ferma la porte, ajusta son châle et fit une caresse à son pékinois au joli nom de Moebius. Elle n’avait pas besoin des cartes, « je connais bien la place et je vais le cramer, ce ne sera pas du gâteau, mais il ne perd rien pour attendre ».
« Bip, bip » sonna son portable, la voix quasi inaudible de son ami Al-Huwarizmi se fit entendre. Al était son cousin germain, d’origine persane, habile cavalier. « Descend de ton cheval ! », s’exclama- t-elle, « je t’entends mal ». Le cavalier rit au plaisir de l’entendre. « Rejoins-moi dès que possible à la croix. », sans un mot de plus, il raccroche. Encore un peu choquée, Sophie poussa son autoradio, « sans doute un piano Steiner » pensa-t-elle.
Elle tourna à droite après la grange. « Mais quel rôle ont donc joué Robert le bègue et le jeune chauffeur de taxi responsable de la mort de John Nash ? » Le chauffeur avait peu l’air honnête et Sophie ne pensait pas que Robert vaille mieux… c’était honteux une bande de sales gosses.
Sophie quitta sa voiture avec son pékinois, «ne tire pas sur ta laisse, Moebius », Al n’est pas loin… Les retrouvailles furent émouvantes et Al a tout expliqué : encore un coup monté par Nash, pas l’ombre d’un doute, pas de mafia, c’était bien un accident de la route.
Voici la solution tant attendue du jeu « La récré des maths » précédente !
Êtes-vous d’accord que les trapèzes mauves sont tous les mêmes ? Et les triangles orange aussi ? Alors pourquoi arrive-t-on à un résultat impossible : aire du rectangle de gauche = aire du rectangle de droite donc 64 = 65 ?
Ce paradoxe est en fait une illusion d’optique !
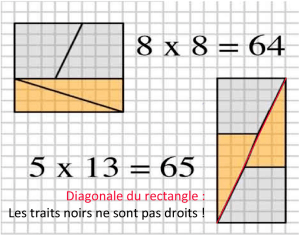
Dans le deuxième rectangle, les pièces se superposent un peu : la pente des triangles est plus forte (8/3 ≈ 2,66) que celle des trapèzes (5/2 = 2,5) donc le trait en diagonale n’est pas une droite !

